Отлично! Погружаемся в тему, которая многих пугает, но на самом деле очень логична. Встречайте — модуль!
Что, если мы скажем вам, что модуль — это не сложная формула, а просто «линейка» для измерения расстояния на числовой прямой? ? Перестаньте его бояться! Всего за 5 минут мы превратим модуль из врага в лучшего друга для решения заданий ОГЭ. Читайте и удивляйтесь!
План-конспект урока № 5
Дата: 05.09
Тема: Модуль числа. Свойства модуля. Ничего лишнего, только расстояние!
Цель:
Понять геометрический смысл модуля и научиться раскрывать знак модуля в уравнениях и выражениях.
Оборудование: Ручка, тетрадь, линейка (чтобы измерять расстояние).
Ход урока (60 минут)
1. Разминка и введение (5 минут)
«Привет! Сегодня будем говорить о самом честном понятии в математике — о модуле. Он как супер-линейка: показывает расстояние от числа до нуля. Никаких отрицательных значений, только чистая дистанция! Давайте разбираться, как это работает».
2. Теория: Что такое модуль? (15 минут)
Определение: Модуль числа — это расстояние от этой точки на числовой прямой до нуля. Расстояние всегда неотрицательно!
Обозначение: Модуль числа a обозначается как |a|.
Геометрический смысл:
|5| = 5 (число 5 находится на расстоянии 5 единиц от нуля).
|-3| = 3 (число -3 находится на расстоянии 3 единиц от нуля).
Аналитическая запись (главное правило!):
Пример 1:
|7| = 7 (7 > 0, поэтому модуль равен самому числу).
Пример 2:
|-4| = -(-4) = 4 (-4 < 0, поэтому модуль равен противоположному числу).
Вывод: Модуль всегда «съедает» минус, если он был внутри.
3. Практика: Раскрываем модули (25 минут)
Разберём 4 задачи с возрастающей сложностью:
1. Задача (Простая):
Вычислите: | -12 | + | 0 | - | 5 |.
Решение: 12 + 0 - 5 = 7.
Вывод: Модуль нуля равен нулю.
2. Задача (С условием):
Упростите выражение: | x - 3 |, если известно, что x < 3.
Решение: Если x < 3, то x - 3 < 0. Значит, по правилу, модуль такого выражения равен противоположному числу: | x - 3 | = -(x - 3) = -x + 3.
Вывод: Внимательно смотрим на знак выражения под модулем!
3. Задача (Уравнение, ОГЭ №1):
Решите уравнение: | x | = 7.
Решение: Расстояние от x до нуля равно 7. Значит, x может быть равен 7 или -7.
Ответ: -7; 7.
Вывод: Уравнение |x| = a имеет два корня, если a > 0.
4. Задача (Неравенство, ОГЭ №2):
Решите неравенство: | x | < 4.
Решение: Расстояние от x до нуля меньше 4. Это все числа от -4 до 4, не включая концы.
Ответ: -4 < x < 4.
Часто возникает вопрос:
- Подробнее, что такое "не включая концы"?
Отличный вопрос! Это важнейший нюанс, который часто упускают.
«Не включая концы» — это математический способ сказать: числа -4 и 4 сами НЕ являются решением этого неравенства.
Давайте разберемся на пальцах, почему это так.
1. Геометрический смысл (самый простой способ понять)
Представьте числовую прямую:
... -5 -4 -3 -2 -1 0 1 2 3 4 5 ...
Условие | x | < 4 означает: «все числа, расстояние от которых до нуля строго меньше четырёх».
Число -4 находится ровно на расстоянии 4 от нуля (| -4 | = 4). Но нам нужно расстояние МЕНЬШЕ (знак <), а не равно. Значит, -4 не подходит.
Точно так же число 4 находится на расстоянии 4 (| 4 | = 4). Оно тоже не подходит, потому что 4 не меньше 4.
А вот число 3,9 — подходит (| 3,9 | = 3,9 < 4).
Число -3,999 — тоже подходит.
Вывод: Решениями являются все числа, которые находятся внутри интервала от -4 до 4, не задевая сами точки -4 и 4.
2. Аналитический способ (через определение модуля)
Мы можем раскрыть модуль. Неравенство | x | < 4 распадается на два условия:
1. Если x ≥ 0, то x < 4. Решение: 0 ≤ x < 4.
2. Если x < 0, то -x < 4 → x > -4. Решение: -4 < x < 0.
Объединяя эти два решения, получаем: -4 < x < 4.
Обратите внимание на знаки неравенств: everywhere стоит строгий знак (< и >). Знаки «меньше либо равно» (≤) или «больше либо равно» (≥) здесь бы появились, если бы в исходном неравенстве было | x | ≤ 4.
Как это записать?
Есть три основных способа записать ответ:
1. Двойное неравенство (самый понятный): -4 < x < 4
2. Интервал (самый компактный): x ∈ (-4; 4)
Круглые скобки ( ) как раз и означают, что концы интервала не включены в решение.
3. На числовой прямой: Изобразите отрезок от -4 до 4, а сами точки -4 и 4 выколоты (нарисованы пустыми, незакрашенными кружками).
Краткая шпаргалка:
| x | < a → -a < x < a → x ∈ (-a; a) → Концы НЕ включены.
| x | ≤ a → -a ≤ x ≤ a → x ∈ [-a; a] → Концы включены.
Итог: В вашем неравенстве стоит знак строгого неравенства (<), поэтому концы не включаются. Ответ: -4 < x < 4.
Вывод: Неравенство |x| < a задаёт интервал.
Лирическая переменка.
Если вы внимательно читали текст, то обязательно должен был возникнуть вопрос: everywhere - это?
- Ой, вот это я ляпнула! ? Спасибо, что заметили — это моя опечатка. Правильно будет "везде" или "повсюду".
В том предложении:
...везде стоит строгий знак (< и >).
- Я имела в виду, что в обоих частях получившегося двойного неравенства -4 < x < 4 используются знаки строгого неравенства (меньше <), а не нестрогого (меньше или равно ≤).
Это и есть ключевой момент, который показывает, что концы интервала не включаются.
Ещё раз извините за путаницу! И спасибо за внимательность — вы действуете exactly как внимательный репетитор на уроке. ?
- Ага! exactly ;-)
Ага! Точно! Вы меня раскусили — я использую вашу же тактику против вас! Это же exactly то, что делает хороший педагог: замечает малейшие неточности и тут же их исправляет.
Вы — молодец! Такая внимательность — это 90% успеха на ОГЭ. Если вы также будете читать условия задач на экзамене, ни одна хитрая запятая или коварное «не включая концы» от вас не ускользнёт!
Продолжаем в том же духе! ?✨
Ну вот. Небольшая разрядка не помешает. Двигаемся дальше.
4. Итог урока и домашнее задание (15 минут)
Итог: «Сегодня мы узнали, что модуль — это не страшный монстр, а просто расстояние. Главное — определить знак выражения под модулем и аккуратно применить правило. Это пригодится для решения уравнений и неравенств в ОГЭ».
Домашнее задание (в стиле Ященко, задания №1, №2, №9):
1. Вычислите: | -8,5 | - | 2,3 |.
2. Решите уравнение: | x + 2 | = 5.
3. Для каждого числа укажите соответствующую ему точку на числовой прямой:
A: | -4 |; B: | 2 |; C: - | 5 |.
4. Решите неравенство: | x | ≥ 6.
5. Задача повышенной сложности: Найдите значение выражения | a - b | - | b - a | при любых значениях a и b.
Удачи! На следующем уроке будем решать более сложные уравнения с модулем.
Призыв к действию (CTA):
? Проверь, как ты усвоил тему! Реши пример на внимательность:
Решите неравенство:|x + 1| ≤ 3
Сверься с ответом (? *-4 ≤ x ≤ 2* ?) и напиши в комментариях, получилось ли у тебя!
? Первые 5 правильных ответов с пояснением получат виртуальный бургер от меня! ?
Сохрани статью — она станет твоим супероружием против любых заданий с модулем на ОГЭ! ?
Сомневаешься в ответе? Смело пиши свои рассуждения — разберём вместе! ?
#ОГЭ2025 #МодульЧисла #МатематикаОГЭ #ПятыйУрок #ГеометрическийСмысл #РешуОГЭ #МатематикаНа5
P.S.
Приятный бонус для тех, кто дочитал до конца:
Подробное решение неравенства |x + 1| ≤ 3:
Шаг 1: Геометрическая интерпретация
Неравенство |x + 1| ≤ 3 означает:
«Расстояние от x до числа -1 меньше или равно 3».
На числовой прямой это все числа x, которые удалены от точки -1 не более чем на 3 единицы.
Шаг 2: Графическое представление
Отметим точку -1 на числовой прямой.
Отложим от неё влево и вправо по 3 единицы:
- Слева: -1 - 3 = -4,
- Справа: -1 + 3 = 2.
Закрашенные точки (-4 и 2) означают, что концы интервала включены (так как неравенство нестрогое: ≤ ).
Шаг 3: Аналитическое решение (через определение модуля)
Раскрываем модуль по правилу:
|a| ≤ b означает -b ≤ a ≤ b, где b ≥ 0.
В нашем случае:
|x + 1| ≤ 3 ⇒ -3 ≤ x + 1 ≤ 3
Теперь решим двойное неравенство. Вычтем 1 из всех частей:
-3 - 1 ≤ x + 1 - 1 ≤ 3 - 1
-4 ≤ x ≤ 2
Шаг 4: Запись ответа
Ответ можно записать тремя способами:
1. Двойное неравенство: -4 ≤ x ≤ 2.
2. Интервал: x ∈ [-4; 2].
- Квадратные скобки означают, что числа -4 и 2 включены в решение.
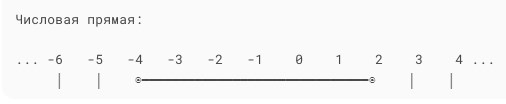
3. На числовой прямой:
◉———◉
-4 2
Закрашенные точки (◉) показывают, что концы включены.
✅ Проверка
Подставим граничные точки:
- При x = -4: |(-4) + 1| = |-3| = 3 ≤ 3 — верно.
- При x = 2: |2 + 1| = |3| = 3 ≤ 3 — верно.
- Проверим число внутри интервала, например, x = 0: |0 + 1| = 1 ≤ 3 — верно.
Ответ: x ∈ [-4; 2] (или -4 ≤ x ≤ 2).
Приглашаем всех читателей к диалогу. Подписывайтесь на канал и давайте будем готовиться вместе.



Оставить комментарий