Отлично! Переходим к одной из самых мощных тем в алгебре — степеням. Готовьтесь умножать числа с суперсилой!
Что, если мы скажем вам, что отрицательная степень — это не ошибка, а суперспособность числа? Она не делает его меньше, а просто «переворачивает»! Узнайте, как всего одно правило решит половину заданий ОГЭ на степени. Добро пожаловать в мир математической магии! ✨
План-конспект урока №6
Дата: 06.09
Тема: Степени с целым показателем. Умножение, деление и возведение в степень с помощью одного правила!
Цель:
Понять, что такое степень с целым (в т.ч. отрицательным) показателем, и научиться применять свойства степеней для упрощения выражений.
Ход урока (60 минут)
1. Разминка и введение (5 минут)
«Привет! Сегодня будем говорить о степенях — это как суперспособность для чисел. Если число умножается само на себя, это можно записать короче. А если оно в минусовой степени? Это не страшно, это просто его «зеркальная копия»! Давайте разбираться».
2. Теория: Что такое степень? (15 минут)
Важные случаи:
Вывод:
Отрицательная степень не делает число отрицательным! Она просто переносит его в знаменатель.
3. Свойства степеней (главные правила)
Эти правила позволяют легко манипулировать степенями:
4. Практика: Решаем примеры (25 минут)
Разберём 4 задачи с возрастающей сложностью:
5. Итог урока и домашнее задание (15 минут)
Итог:
«Сегодня мы узнали, что степени — это не страшно. Отрицательный показатель просто «переворачивает» дробь, а свойства степеней позволяют легко упрощать выражения. Главное — следить за основаниями!»
Домашнее задание (в стиле Ященко, задания №1, №2, №4):
Бонус для терпеливых
Объясним, как решать задачу № [5] из домашнего задания. Подробно разберём алгоритм и типичные ошибки. Ответ должен быть понятен даже не самому сильному ученику.
Шаг 1: Превращаем отрицательные степени в обыкновенные дроби
Помним золотое правило:
Отрицательная степень = «перевернуть» дробь с положительной степенью.
Шаг 2: Сравниваем дроби с одинаковыми числителями
У обеих дробей числитель равен 1.
Правило:
Из двух дробей с одинаковыми числителями больше та, у которой знаменатель меньше.
- Знаменатель первой дроби: 8
- Знаменатель второй дроби: 9
8 < 9, значит:
1/8>1/9
Шаг 3: Возвращаемся к исходным выражениям
Так как:
? Типичные ошибки, которые нельзя допускать!
- Сравнивают отрицательные степени как положительные числа
- Путают дроби с разными знаменателями
- Забывают, что сравнение дробей обратно сравнению знаменателей
? Совет для проверки
Можно посчитать десятичные значения:
Вывод:
Всегда переводите отрицательные степени в дроби — это снимает все вопросы!
Удачи! На следующем уроке будем применять степени в более сложных выражениях.
Призыв к действию (CTA):
 Запутался? Смело пиши свой ход мыслей
Запутался? Смело пиши свой ход мыслей
? Проверь, как ты усвоил суперсилу степеней! Реши пример на скорость:
Сверься с ответом (? *1* ?) и напиши в комментариях, сколько секунд у тебя это заняло!
? Первые 10 решивших получают виртуальную пиццу за скорость! ?
Сохрани статью — она станет твоим тайным оружием против любых степеней на ОГЭ! ?
P.S. Запутался? Смело пиши свой ход мыслей — разберём вместе и найдём ошибку!
#ОГЭ2025 #Степени #МатематикаОГЭ #ШестойУрок #ОтрицательнаяСтепень #РешуОГЭ #МатематикаНа5








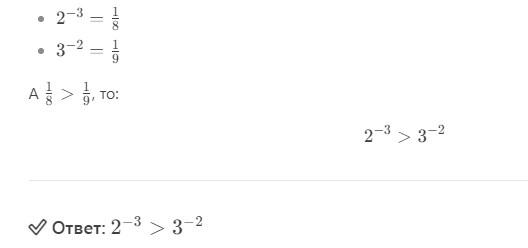



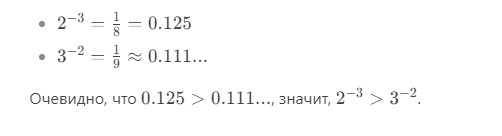
Оставить комментарий